Question

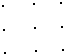在3×3的矩阵中，一共可以套出

76

个不同的三角形？

Answer 1

分析：此题属于钉子数计数问题，可以实际操作，边操作边计数的方法，得出答案，也可以把相邻的点都连成线，用数三角形的方法，得出答案．

解答：解：拿一个橡皮筋，进行实际操作，
（1）一行中的两颗钉子与邻行的一颗钉子组成的三角形的个数是：6×4=24，
（2）一行中的两颗钉子与隔一行的一颗钉子组成的三角形的个数是：6×2×2=24，
（3）一行中的三颗钉子与邻行的一颗钉子组成的三角形的个数是：3×4×2=24，
（4）一行中的三颗钉子与隔一行的一颗钉子组成的三角形的个数是：24-20=4，
24+24+24+4=76，
所以一共可以套出76个不同的三角形；
故答案为：76．

点评：解答此题的关键是，不管用哪种方法计数，在计数时，一定要有顺序的进行，做到不重复，不遗漏，即可解答，直接用C₉³-8（同一直线上的三点）也可．