Question

在右上图中，已知矩形GHCD的面积是矩形ABCD面积的

1

4

，矩形MHCF的面积是矩形ABCD面积的

1

6

，矩形BCFE的面积等于3平方米．矩形AEMG的面积等于

 

平方米．

Answer 1

分析：如图所示：

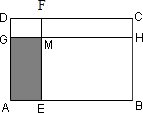
等宽的长方形的面积比就等于对应长的比，从而可以得出长方形DGMF的面积是ABCD的

1

12

，
则长方形MHCF的面积与DGMF的面积比是2：1；
同理可得：MH=2MG，长方形BHME的面积是AEMG的 2 倍；
进而得出阴影部分是长方形的面积的几分之几，问题即可得解．

解答：解：长方形DGMF的面积是ABCD的

1

4

-

1

6

=

1

12

，
则长方形MHCF的面积是DGMF的

1

6

÷

1

12

=2 倍；
可得：MH=2MG，长方形BHME的面积是AEMG的 2 倍；
所以，长方形AEMG的面积是ABHG的

1

1+2

=

1

3

，
而且，长方形ABHG的面积是ABCD的 1-

1

4

=

3

4

，
可得：长方形AEMG的面积是ABCD的

3

4

×

1

3

=

1

4

；
则有：长方形BCFE的面积是ABCD的 1-

1

12

-

1

4

=

2

3

，
可得：长方形ABCD的面积是 3÷

2

3

=4.5 平方米，
则有：阴影长方形AEMG的面积是 4.5×

1

4

=1.125 平方米．
故答案为：1.125．

点评：推论得出：阴影长方形AEMG的面积是长方形ABCD的面积的

1

4

，是解答本题的关键．