Question

如图，将△BAC绕点C按顺时针方向旋转30°，得到△B′A′C，若AC⊥A′B′，则∠BAC的度数是________．

Answer 1

60°
分析：在平面内，将一个图形绕着一个定点沿某个方向转动一个角度，这样的图形运动称为旋转．这个定点称为旋转中心，转动的角称为旋转角，旋转不改变图形的大小和形状．

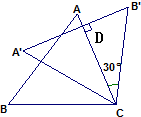
解答：若AC⊥A′B′交与D点，在△CDB'中，∠B'=180°-90°-30°=60°
因为旋转不改变图形的大小和形状，所以∠BAC=∠B'=60°．
故答案为：60°．
点评：旋转的特征：①旋转前后，两个图形的对应点到旋转中心的距离相等；
②对应点与旋转中心的连线所成的旋转角彼此相等；
③旋转变化前后，对应线段、对应角分别相等，旋转不改变图形的大小和形状．