题目内容
 直角梯形ABCD的上底是18厘米,下底是27厘米,高是24厘米(如图).请你过梯形的某一个顶点画两条直线,把这个梯形分成面积相等的三部分(要求写出解答过程,画出示意图,图中的有关线段要标明长度).
直角梯形ABCD的上底是18厘米,下底是27厘米,高是24厘米(如图).请你过梯形的某一个顶点画两条直线,把这个梯形分成面积相等的三部分(要求写出解答过程,画出示意图,图中的有关线段要标明长度).分析:把直角梯形分成三部分后每部分的面积是[(18+27)×24]÷2÷3=180(平方厘米).又三角形的面积=底×高×
.
由于180÷18÷
=20厘米,180÷24÷
=15厘米,由此在CD上截取CE=20厘米,在AD上截取AF=15厘米.连接BE,BF,就可以把这个梯形平均分成三部分.这时S△BCE=
×20×18=180(平方厘米),S△ABF=
×15×24=180(平方厘米),S四边形BFDE=
×(27+18)×24-180-180=180(平方厘米).
如图:
| 1 |
| 2 |
由于180÷18÷
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
如图:

解答:解:[(18+27)×24]÷2÷3=180(平方厘米).
那么,在CD上截取CE=20厘米,在AD上截取AF=15厘米.连接BE,BF,就可以把这个梯形平均分成三部分.
这时S△BCE=
×20×18=180(平方厘米),
S△ABF=
×15×24=180(平方厘米),
S四边形BFDE=
×(27+18)×24-180-180=180(平方厘米). 如图:
如图:
那么,在CD上截取CE=20厘米,在AD上截取AF=15厘米.连接BE,BF,就可以把这个梯形平均分成三部分.
这时S△BCE=
| 1 |
| 2 |
S△ABF=
| 1 |
| 2 |
S四边形BFDE=
| 1 |
| 2 |
 如图:
如图:点评:在求出平均每个图形面积的基础上,根据三解形的面积公式求出在相应边上应截取线段的长度是完成本题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 如图,直角梯形ABCD的上底BC=8厘米,下底AD=13厘米,高CD=6厘米,且三角形ABF、三角形BCE和四边形BEDF的面积相等.求三角形DEF的面积.
如图,直角梯形ABCD的上底BC=8厘米,下底AD=13厘米,高CD=6厘米,且三角形ABF、三角形BCE和四边形BEDF的面积相等.求三角形DEF的面积. 如图,直角梯形ABCD的上底是5厘米,下底是7厘米,高是4厘米,且三角形ADE、ABF和四边形AECF的面积相等,则三角形AEF的面积是
如图,直角梯形ABCD的上底是5厘米,下底是7厘米,高是4厘米,且三角形ADE、ABF和四边形AECF的面积相等,则三角形AEF的面积是 如图,直角梯形ABCD的上底是10厘米,下底AD是14厘米,高CD是5厘米.又三角形ABF、三角形BCE和四边形BEDF的面积相等.求三角形DEF的面积.
如图,直角梯形ABCD的上底是10厘米,下底AD是14厘米,高CD是5厘米.又三角形ABF、三角形BCE和四边形BEDF的面积相等.求三角形DEF的面积. 如图,已知直角梯形ABCD的上底长18厘米,下底长27厘米,高24厘米,三角形ABF、三角形ADE和四边形AECF面积相等.求三角形AEF的面积.
如图,已知直角梯形ABCD的上底长18厘米,下底长27厘米,高24厘米,三角形ABF、三角形ADE和四边形AECF面积相等.求三角形AEF的面积.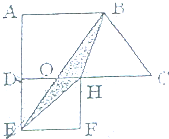 如图,直角梯形ABCD的上底和高相等,正方形DEFH的边长是6厘米,阴影部分的面积是多少平方厘米?
如图,直角梯形ABCD的上底和高相等,正方形DEFH的边长是6厘米,阴影部分的面积是多少平方厘米?