题目内容
47名同学参加了数学和语文考试，两门都没得100分的有26人，数学得满分的有17人，语文得百分的有12人，试问两门都得100分的有几人？
考点：容斥原理
专题：传统应用题专题
分析：两门都没得100分的有26人，那么至少一门得100分的就是47-26=21人，由此根据语文、数学得100分的人数画图分析：
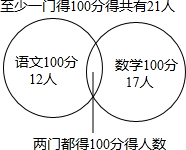
由此利用容斥原理即可求出两门都得100分的人数．
由此利用容斥原理即可求出两门都得100分的人数．
解答：
解：至少一门得100分的有：47-26=21（人），
两门都得100分的有：12+17-21=8（人），
答：两门都得100分的有8人．
两门都得100分的有：12+17-21=8（人），
答：两门都得100分的有8人．
点评：此题考查了利用容斥原理解答问题的灵活应用，这里求出至少一门得100分的人数是解决问题的关键．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目