题目内容
 将三角形ABC,AB四等分,BC五等分,AC三等分(如下图所示)那么,
将三角形ABC,AB四等分,BC五等分,AC三等分(如下图所示)那么,| 三角形DEF的面积 |
| 三角形ABC的面积 |
| 5 |
| 12 |
| 5 |
| 12 |
分析:要求
的比,可先求出
、
、
的比值;从而求出
的比值,再利用1减去这个比值,即可解决问题.
(1)连接AF,因为D是AC的三等分点,根据高一定时,三角形的面积与底成正比例的性质可得:三角形DFC=
三角形AFC;因为F是BC的五等分点,所以三角形AFC=
三角形ABC;所以可得:三角形DFC=
×
三角形ABC=
三角形ABC;
(2)连接BD、CE,同理可得:三角形ADE=
×
=
三角形ABC;三角形BEF=
×
三角形ABC=
三角形ABC;
(3)三角形DFC、三角形ADE、三角形BEF占三角形ABC的:
+
+
=
,由此即可解决问题.

| 三角形DEF的面积 |
| 三角形ABC的面积 |
| 三角形ADE |
| 三角形ABC |
| 三角形BEF |
| 三角形ABC |
| 三角形DCF |
| 三角形ABC |
| 三角形ADE+三角形BEF+三角形DCF |
| 三角形ABC |
(1)连接AF,因为D是AC的三等分点,根据高一定时,三角形的面积与底成正比例的性质可得:三角形DFC=
| 2 |
| 3 |
| 1 |
| 5 |
| 2 |
| 3 |
| 1 |
| 5 |
| 2 |
| 15 |
(2)连接BD、CE,同理可得:三角形ADE=
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 4 |
| 5 |
| 1 |
| 5 |
(3)三角形DFC、三角形ADE、三角形BEF占三角形ABC的:
| 2 |
| 15 |
| 1 |
| 4 |
| 1 |
| 5 |
| 7 |
| 12 |

解答:解:连接AF、BD、CE:
(1)因为D是AC的三等分点,根据高一定时,三角形的面积与底成正比例的性质可得:三角形DFC=
三角形AFC;又因为F是BC的五等分点,所以三角形AFC=
三角形ABC;
所以可得:三角形DFC=
×
三角形ABC=
三角形ABC;
(2)同理可得:三角形ADE=
×
=
三角形ABC;
三角形BEF=
×
三角形ABC=
三角形ABC;
(3)三角形DFC、三角形ADE、三角形BEF的面积之和占三角形ABC面积的:
+
+
=
,
所以,
=1-
=
;
答:
=
.
故答案为:
.
(1)因为D是AC的三等分点,根据高一定时,三角形的面积与底成正比例的性质可得:三角形DFC=
| 1 |
| 3 |
| 1 |
| 5 |
所以可得:三角形DFC=
| 2 |
| 3 |
| 1 |
| 5 |
| 2 |
| 15 |
(2)同理可得:三角形ADE=
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
三角形BEF=
| 1 |
| 4 |
| 4 |
| 5 |
| 1 |
| 5 |
(3)三角形DFC、三角形ADE、三角形BEF的面积之和占三角形ABC面积的:
| 2 |
| 15 |
| 1 |
| 4 |
| 1 |
| 5 |
| 7 |
| 12 |
所以,
| 三角形DEF的面积 |
| 三角形ABC的面积 |
| 7 |
| 12 |
| 5 |
| 12 |
答:
| 三角形DEF的面积 |
| 三角形ABC的面积 |
| 5 |
| 12 |
故答案为:
| 5 |
| 12 |
点评:此题主要考查了高一定时,三角形的面积与底成正比例的性质的灵活应用,这里要注意灵活使用辅助线.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
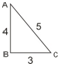 如图,将直角三角形ABC以AB为轴旋转一周,得到的圆锥体积是V,那么V=( )
如图,将直角三角形ABC以AB为轴旋转一周,得到的圆锥体积是V,那么V=( )| A、12π | B、36π | C、48π |
 图中,直角三角形ABC 的两条直角边AB 和BC 的长度分别为3和4,将三角形ABC绕点C顺时针旋转至A1B1C,使得A1C与B1C在直线l上.
图中,直角三角形ABC 的两条直角边AB 和BC 的长度分别为3和4,将三角形ABC绕点C顺时针旋转至A1B1C,使得A1C与B1C在直线l上. 将三角形ABC的AB边延长到D,BC边延长到E,CA边延长到F,使DB=2AB,EC=2BC,FA=2AC,如果三角形ABC的面积是5平方厘米,那么三角形DEF的面积是多少平方厘米?
将三角形ABC的AB边延长到D,BC边延长到E,CA边延长到F,使DB=2AB,EC=2BC,FA=2AC,如果三角形ABC的面积是5平方厘米,那么三角形DEF的面积是多少平方厘米?