题目内容
4. 下面是5路公共汽车从将军路站到红萍路站的行驶情况.
下面是5路公共汽车从将军路站到红萍路站的行驶情况.(1)5路公共汽车出发3分后达到最高速度,8分到达红萍.
(2)5路公共汽车在路上有4分是匀速行驶.
分析 这是一个折线统计图,纵轴数据表示汽车速度,每格表示10千米,横轴上的数据表示时间,每格表示1分,从图中可以看出:
(1)5路公共汽车出发3分后达到最高速度,8分到达红萍.
(2)5路公共汽车,汽车行驶速度从开始到3分钟速度速度逐渐增快,从3分钟到7分钟速度最快,最高速度是40千米/时;从7分钟到8分钟速度渐慢,直到停止.
解答 解:1)5路公共汽车出发3分后达到最高速度,8分到达红萍.
(2)5路公共汽车在路上有4分是匀速行驶.
故答案为:3,8,4.
点评 解决本题关键是看懂折线统计图,能从图中找出汽车速度的变化.

练习册系列答案
相关题目
14.探究分析
我们已经知道三角形的内角和是180°,我们可以用这个知识求出四边形、五边形、六边形内角和的度数,进而探索出多边形的内角和.
①阅读表格中的内容并填空.
②根据四边形、五边形、六边形内角和的计算方法,归纳出n边形的内角和:n边形的内角和=180°(n-2)(用含有字母n的式子表示).
③若某多边形的内角和是1440°,利用前面探究的结论计算这个多边形的边数.
我们已经知道三角形的内角和是180°,我们可以用这个知识求出四边形、五边形、六边形内角和的度数,进而探索出多边形的内角和.
| 多 边 形 | 内角和的度数 |
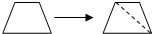 | 180°×2=360° |
 | 180°×3=540° |
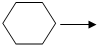 |
②根据四边形、五边形、六边形内角和的计算方法,归纳出n边形的内角和:n边形的内角和=180°(n-2)(用含有字母n的式子表示).
③若某多边形的内角和是1440°,利用前面探究的结论计算这个多边形的边数.
14.如果x÷$\frac{3}{5}$=y×$\frac{5}{7}$=z÷$\frac{7}{9}$(x、y、z都是非零自然数),那么( )
| A. | x>y>z | B. | y>z>x | C. | y>x>z | D. | z>y>x |