题目内容
如图,四边形ABCD是平行四边形,BE:EC=1:2,F是DC的中点,三角形ABE的面积是12cm2,那么三角形ADF的面积是

18
18
cm2.
分析:F是DC的中点,所以三角形ADF的面积是三角形ACD面积的
,而三角形ACD面积的面积等于平行四边形面积的
,所以以三角形ADF的面积等于平行四边形面积的
×
=
;又因为BE:EC=1:2,三角形ABE和三角形AEC等高,所以三角形ABE和三角形AEC的面积比是:1:2,因此三角形ABC的面积是:12×(2+1)=36平方厘米,那么平行四边形面积的是36×2=72平方厘米,所以三角形ADF的面积是:72×
=18(平方厘米).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:三角形ACF和三角形AFD等底等高,所以三角形ADF的面积是三角形ACD面积的
,
三角形ADF的面积等于平行四边形面积的
×
=
;
三角形ABE和三角形AEC的面积比是:1:2,因此三角形ABC的面积是:12×(2+1)=36(平方厘米),
那么平行四边形面积的是:36×2=72(平方厘米),
所以三角形ADF的面积是:72×
=18(平方厘米);
答:三角形ADF的面积是18cm2.
故答案为:18.
| 1 |
| 2 |
三角形ADF的面积等于平行四边形面积的
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
三角形ABE和三角形AEC的面积比是:1:2,因此三角形ABC的面积是:12×(2+1)=36(平方厘米),
那么平行四边形面积的是:36×2=72(平方厘米),
所以三角形ADF的面积是:72×
| 1 |
| 4 |
答:三角形ADF的面积是18cm2.
故答案为:18.
点评:此题考查了等高三角形的面积比等于底的比的性质,即高一定时,三角形的面积与底成正比的关系的灵活应用;这种题往往是通过“转化”解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图平行四边形ABCD的面积是36平方厘米,其中AE=
如图平行四边形ABCD的面积是36平方厘米,其中AE= 如图,四边形ABCD内有一点O,且O点到四条边AB、BC、CD、AD的距离都等于8厘米.若四边形ABCD的周长是62厘米.那么,四边形ABCD的面积是
如图,四边形ABCD内有一点O,且O点到四条边AB、BC、CD、AD的距离都等于8厘米.若四边形ABCD的周长是62厘米.那么,四边形ABCD的面积是 如图,四边形ABCD的周长是60厘米,点M到各边的距离都是4.5厘米,这个四边形的面积是
如图,四边形ABCD的周长是60厘米,点M到各边的距离都是4.5厘米,这个四边形的面积是 如图,四边形ABCD是边长为8厘米的正方形,三角形ADF的面积比三角形CEF
如图,四边形ABCD是边长为8厘米的正方形,三角形ADF的面积比三角形CEF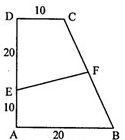 如图,四边形ABCD是直角梯形,∠A=∠D=90?,点E将DA分成2:1,F为BC中点,则四边形FEAB的面积为
如图,四边形ABCD是直角梯形,∠A=∠D=90?,点E将DA分成2:1,F为BC中点,则四边形FEAB的面积为