题目内容
如图，△ABC中，E是AD的中点，已知△ABC的面积是2，△BEF的面积是
，求△AEF的面积。
，求△AEF的面积。
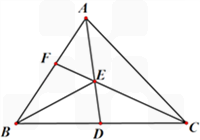
（1）因为AE=DE，
所以S△AEC=S△DEC，S△AEB=S△DEB；
那么S△ABC=2S△DEC+2S△DEB=2，
所以S△DEC+S△DEB=S△BCE=1，
又因为S△BEF=
，所以S△BCF=S△BCE+S△BEF=1+
=
，
则S△ACF=S△ABC﹣S△BCF=2﹣
=
；
（2）因为BF：AF=S△BCF+S△ACF=
：
=2：1，
所以S△BEF：S△AEF=2：1，
所以S△AEF=
×1÷2=
所以△AEF的面积是
。
所以S△AEC=S△DEC，S△AEB=S△DEB；
那么S△ABC=2S△DEC+2S△DEB=2，
所以S△DEC+S△DEB=S△BCE=1，
又因为S△BEF=
，所以S△BCF=S△BCE+S△BEF=1+=，则S△ACF=S△ABC﹣S△BCF=2﹣
=；（2）因为BF：AF=S△BCF+S△ACF=
：=2：1，所以S△BEF：S△AEF=2：1，
所以S△AEF=
×1÷2=所以△AEF的面积是
。
练习册系列答案
相关题目
如图，△ABC中，E是AD的中点，已知△ABC的面积是2，△BEF的面积是
如图三角形ABC中，E为AC之中点．BD=2DC，AD与BE交于F，则三角形BDF的面积：四边形DCEF的面积=
如图，△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB=6cm．求△DEB的周长．