题目内容
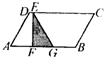 如图,平行四边形ABCD的面积是72平方厘米,E是CD边上的任一点,AF=FG=GB,则阴影部分的面积是
如图,平行四边形ABCD的面积是72平方厘米,E是CD边上的任一点,AF=FG=GB,则阴影部分的面积是12
12
平方厘米.分析:由图知:阴影部分的面积是指△EFG的面积,?ABCD与△EFG等高,,又因AF=FG=GB,可得FG=
AB,根据平行四边形和三角形的面积找出等量关系式,即可算出△EFG的面积.
| 1 |
| 3 |
解答:解:因为平行四边形ABCD的面积=AB×高,
平行四边形ABCD的面积是72平方厘米,
所以AB×高=72,
因为AF=FG=GB,
所以FG=
AB,
所以S△EFG的高等于平行四边形ABCD的高,
又因为S△EFG=FG×高×
,
所以S△EFG=
AB×高×
,
=72×
,
=12(平方厘米).
答:阴影部分的面积是 12平方厘米.
故答案为:12.
平行四边形ABCD的面积是72平方厘米,
所以AB×高=72,
因为AF=FG=GB,
所以FG=
| 1 |
| 3 |
所以S△EFG的高等于平行四边形ABCD的高,
又因为S△EFG=FG×高×
| 1 |
| 2 |
所以S△EFG=
| 1 |
| 3 |
| 1 |
| 2 |
=72×
| 1 |
| 6 |
=12(平方厘米).
答:阴影部分的面积是 12平方厘米.
故答案为:12.
点评:此题重点找准三角形EFG和平行四边形ABCD等高,并且三角形EFG的底等于平行四边形ABCD的底的三分之一.

练习册系列答案
相关题目
 如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是
如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是 如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度.
如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度. 如图,平行四边形中相邻两边AB:AD=4:3,如果AD=4.5厘米,那么AB的长度是
如图,平行四边形中相邻两边AB:AD=4:3,如果AD=4.5厘米,那么AB的长度是 (2010?邯山区)已知如图,平行四边形ABCD的边AB是半圆O的直径,边AB 的中点O是半圆的圆心,且半圆O的圆周经过点D,DO与AB垂直,垂足是点O,AB=6.求图中阴影部分的面积.
(2010?邯山区)已知如图,平行四边形ABCD的边AB是半圆O的直径,边AB 的中点O是半圆的圆心,且半圆O的圆周经过点D,DO与AB垂直,垂足是点O,AB=6.求图中阴影部分的面积. (2013?华亭县模拟)如图,平行四边形相邻的两条边AB与BC的长度的比是
(2013?华亭县模拟)如图,平行四边形相邻的两条边AB与BC的长度的比是