Question

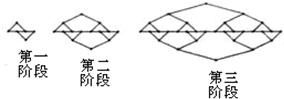如图，有一个图形依某种特定的规律成长，下面分别是第一阶段、第二阶段与第三阶段的图示，试问，当图形成长至第七阶段时有

510

个点．

Answer 1

分析：根据题干，此题可以把图中的点分成两部分进行讨论：即小三角形的点数与每一阶段增加的点两部分．
（1）图中小三角形的个数在每一个阶段存在的规律为：2¹、2²、2³、2⁴…那么在第七阶段，三角形的个数为：2⁷，每个三角形有3个点，那么这些三角形共有2⁷×3=128×3=384个点；
（2）由题干可知，第二阶段增加了2个点，第三阶段增加了2×2+2=6个点，第四阶段增加了6×2+2=14个点，第五阶段增加了14×2+2=30个点，第六阶段增加了30×2+2=62个点，第七阶段增加了62×2+2=126，
有上述推理即可得出第七阶段图形中的点数．

解答：解：根据题干分析可得：
第七阶段小三角形的点数为：2⁷×3=128×3=384（个），
第七阶段增加的点数为：62×2+2=126（个），
384+126=510（个），
答：第七阶段的点数为510个．
故答案为：510．

点评：把图形中的三角形和增加的点数分开来讨论，得出点数的规律是解决本题的关键．