Question

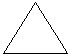
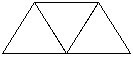
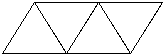
准备若干个边长为1厘米的等边三角形，并按图所示一个接一个地拼接起来，然后填下表．

三角形的个数
拼成图形的周长/厘米

猜想：
（1）当三角形的个数是10时，所拼成图形的周长是

12

厘米．
（2）当三角形的个数是100时，所拼成图形的周长是

102

厘米．

Answer 1

分析：这是一个找规律的题型，只要找出题中周长与个数的关系式，就可求出结果．

解答：解：依题意可知：因为每个边长都是1厘米，
当n=1时，周长=2+1；
当n=2时，周长=2+2；
当n=3时，周长=2+3；
当n=4时，周长=2+4；
…；
当有n个梯形时，图形周长=2+n．
故填表如下：

三角形的个数	1	2	3	4	5	6	7	8
拼成图形的周长/厘米	3	4	5	6	7	8	9	10

（1）当三角形的个数是10时，所拼成图形的周长是2+10=12（厘米）．
（2）当三角形的个数是100时，所拼成图形的周长是2+100=102（厘米）．
故答案为：12；102．

点评：此题考查的知识点是图形数字的变化类问题，关键是观察分析得出梯形个数与图形周长的关系为3n+2=周长．