Question

在一个算式 OLOKO×11=KOALLO 中，不同的字母代表不同数字．那么 KOALLO=

543994

．

Answer 1

分析：把这个乘法算式列出竖式可得：

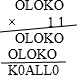
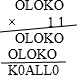
观察竖式可得，O最大是8，若O=8，则K最大是9，则十位上和百位上相加的数字分别是7和8，不符合题意；由此可得十位上和百位上的K+O的和不能进位，则O小于5，若O=4，则K=5，那么L=4+5=9，则49454×11=543994，正好符合题意．

解答：解：根据题干分析可得：49454×11=543994，
答：KOALLO=543994．
故答案为：543994．

点评：解答此题的关键是列出乘法竖式，根据O的取值，求得K、O与L的取值即可解答问题．