题目内容
由6、7、8、9组成的各位数字互不相同的四位数中，能被11整除的数有
8
8
个．分析：能被11整除数的特征是：奇数数位的数字之和减去偶数数位数字之和，所得差能被11整除，这个数就能被11整除，因此6、9如果在千位、十位，则7、8在百位、个位，反之也可，由此写出结果即可．
解答：解：6在千位，9在十位，能被11整除的数有6798，6897；
9在千位，6在十位，能被11整除的数有9768，9867；
8在千位，7在十位，能被11整除的数有8976，8679；
7在千位，8在十位，能被11整除的数有7986，7689；
综上所知，能被11整除的数有8个．
故答案为：8．
9在千位，6在十位，能被11整除的数有9768，9867；
8在千位，7在十位，能被11整除的数有8976，8679；
7在千位，8在十位，能被11整除的数有7986，7689；
综上所知，能被11整除的数有8个．
故答案为：8．
点评：此题主要利用被11整除的特征：奇数数位的数字之和减去偶数数位数字之和，所得差能被11整除，这个数就能被11整除解答此题．
练习册系列答案
相关题目
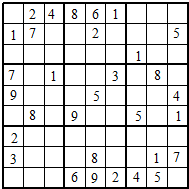9、“九宫阵”是一个9×9的方阵，它是由九个3×3的“九宫格”（图中黑实线围住的方阵）组成．请你在下图中将数字1，2，3，4，5，6，7，8，9分别填入空格内，使得每行、每列及9个“九宫格”中数字1～9均恰好出现一次．当填写完后，那么，位于第4行第4列的数字是（ ）