题目内容
【题目】在三角形ABC中,BD=![]() BC,三角形ABD的面积是30平方厘米,三角形ADE的面积是10平方厘米,求阴影部分的面积为多少平方厘米?
BC,三角形ABD的面积是30平方厘米,三角形ADE的面积是10平方厘米,求阴影部分的面积为多少平方厘米?
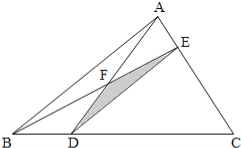
【答案】阴影△DEF的面积是![]() 厘米2
厘米2
【解析】
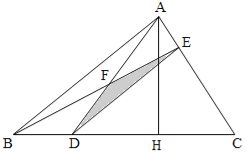
试题分析:过A作AH⊥BC于H,根据高相等的三角形面积之比=底之比可得AE=![]() CE,过D作DG∥AC交BE于G,根据高相等的三角形面积之比=底之比可得S△DEF:S△ADE=DF:AD=
CE,过D作DG∥AC交BE于G,根据高相等的三角形面积之比=底之比可得S△DEF:S△ADE=DF:AD=![]() ,依此即可求解.
,依此即可求解.
解答:解:过A作AH⊥BC于H,则
S△ABD=![]() BDAH,S△ADC=
BDAH,S△ADC=![]() DCAH,
DCAH,
所以S△ABD:S△ADC=BDAH:DCAH=BD:DC(高相等的三角形面积之比=底之比)
因为BD=![]() BC,
BC,
所以BD=![]() DC,
DC,
所以S△ABD:S△ADC=![]() ,
,
又因为S△ABD=30厘米2,
所以S△ADC=60厘米2,
根据高相等的三角形面积之比=底之比
S△ADE:S△ADC=AE:AC
因为S△ADE=10厘米2,
因为S△ADE:S△ADC=![]() ,
,
所以AE:AC=![]() ,
,
所以AE=![]() AC,
AC,
所以AE=![]() CE,
CE,
过D作DG∥AC交BE于G,
则DG:CE=BD:BC=![]() ,
,
所以DG=![]() CE,
CE,
又因为AE=![]() CE,
CE,
所以DG:AE=![]() ,
,
因为DG∥AC,即DG∥AE,
所以DF:AF=DG:AE=![]() ,
,
所以DF:AD=![]() ,
,
所以同样根据高相等的三角形面积之比=底之比有S△DEF:S△ADE=DF:AD=![]() ,
,
因为S△ADE=10厘米2,
S△DEF=![]() ﹙厘米2﹚.
﹙厘米2﹚.
答:阴影△DEF的面积是![]() 厘米2.
厘米2.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目