题目内容
如图中3个图形的体积比是（ ）
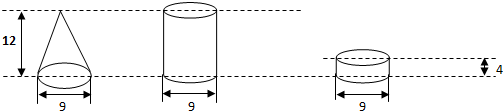
| A、3：9：1 | B、1：9：1 |
| C、1：3：1 |
考点：比的意义,圆柱的侧面积、表面积和体积,圆锥的体积
专题：立体图形的认识与计算
分析：根据题干可得，第一个和第二个图形等底等高，根据等底等高的圆柱的体积是圆锥的体积的3倍可得，圆锥与圆柱的体积之比是1：3，第三个圆柱与第二个圆柱等底，所以它们的体积之比就等于高的比，12：4=3：1，据此即可解答问题．
解答：
解：根据题干分析可得：因为等底等高的圆柱的体积是圆锥的体积的3倍可得，
第一个图形圆锥与第二个图形圆柱的体积之比是1：3，
第三个圆柱与第二个圆柱等底，所以第二个图形与第三个图形的体积之比是12：4=3：1，
所以三个图形的体积之比是：1：3：1．
故选：C．
第一个图形圆锥与第二个图形圆柱的体积之比是1：3，
第三个圆柱与第二个圆柱等底，所以第二个图形与第三个图形的体积之比是12：4=3：1，
所以三个图形的体积之比是：1：3：1．
故选：C．
点评：此题考查了圆柱与圆锥的体积公式的灵活应用．
练习册系列答案
相关题目
把三个边长都是3厘米的正方形拼成一个长方形，这个长方形的面积是（ ）
| A、27c㎡ | B、36c㎡ |
| C、27cm |
下面各数中，（ ）中的0可以去掉．
| A、1027 | B、3.70 |
| C、0.038 |
“73×18”计算结果与（ ）不相等．
| A、73×20-73×2 |
| B、73×3×6 |
| C、73×9+9 |
| D、10×73+8×73 |
以直角三角形的一条直角边的一条直角边为轴，旋转一周，就能得到一个（ ）
| A、圆锥 | B、长方体 | C、圆柱 |
下面三角形中，没有钝角的是（ ）
| A、等腰三角形 | B、等边三角形 |
| C、任意三角形 |