Question

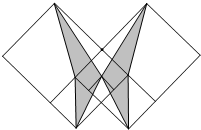如图，大、中、小三个正方形的边长分别为8、4、2，则阴影部分的面积为

 

．

Answer 1

分析：如图所示：作出辅助线，则四边形ABCD是一个梯形，ABCD中的阴影部分的面积就等于梯形的面积减去三角形AHD的面积；四边形BEFC是一个正方形，其中的阴影部分的面积就等于正方形BEFC的面积的一半，据此即可求出阴影部分的面积．

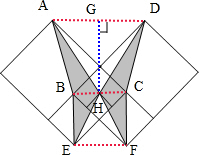
解答：解：如图所示，作出辅助线，
则AD=

82+82

=8

2

，
BC=

42+42

=4

2

AD边上的高HG=8

2

÷2+4

2

÷2=6

2

，
所以阴影部分的面积为：
（8

2

+4

2

）×6

2

÷2-8

2

×6

2

÷2+4

2

×4

2

÷2
=12

2

×6

2

÷2-48+16
=72-48+16
=40．
答：阴影部分的面积是40．
故答案为：40．

点评：此题是一道奥数题，难度较大，需添加多条辅助线，将阴影部分的面积转化成规则图形的面积和或差求解．