题目内容
如图，六个边长为1、2、3的正方形覆盖了一个边长为6的大正方形的一部分，设涂色的部分区域I，大正方形中未被覆盖的部分区域为区域Ⅱ，随机投了一枚硬币，则硬币落在区域I的可能性________落在区域Ⅱ的可能性．（填“＞”“＜”，“=”）
＜
分析：由图形观察可知，边长是3的正方形的覆盖面积是（
+
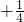）个，边长是2的正方形的覆盖面积是（
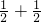）个，边长是1的覆盖面积是个，进一步求出没覆盖的面积，即区域Ⅱ的面积．通过面积的大小比较，判断硬币落下的可能性．
解答：覆盖的面积即区域I的面积：
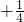（+）×（3×3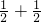）+（）×（2×2）+×（1×1），
=9+4+0.5，
=13.5；
大正方形的面积：
6×6=36；
区域Ⅱ的面积是：
36-13.5=22.5；
区域I＜区域Ⅱ，
所以硬币落在区域I的可能性＜落在区域Ⅱ的可能性．
故答案为：＜．
点评：本题运用正方形的面积公式进行解答，运用覆盖与没覆盖的面积的大小进行判断即可．
分析：由图形观察可知，边长是3的正方形的覆盖面积是（
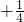+）个，边长是2的正方形的覆盖面积是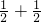（）个，边长是1的覆盖面积是个，进一步求出没覆盖的面积，即区域Ⅱ的面积．通过面积的大小比较，判断硬币落下的可能性．解答：覆盖的面积即区域I的面积：
（
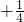+）×（3×3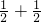）+（）×（2×2）+×（1×1），=9+4+0.5，
=13.5；
大正方形的面积：
6×6=36；
区域Ⅱ的面积是：
36-13.5=22.5；
区域I＜区域Ⅱ，
所以硬币落在区域I的可能性＜落在区域Ⅱ的可能性．
故答案为：＜．
点评：本题运用正方形的面积公式进行解答，运用覆盖与没覆盖的面积的大小进行判断即可．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10、一个棱长为1的小正方体形状的骰子，它的六个面上各写有一个大写英文字母D、E、G、I、N、O中的一个．先将它放在由20个边长为1的小正方形拼成的4×5的棋盘的左上角的小方格上，令字母D朝上（如图所示），然后将它连续的向邻格翻动，并且恰好经过4×5棋盘上的其余的19个小方格各1次（共翻动了19次），最终停止在棋盘的右下角的小方格上．如果图中小方格中给定的字母是骰子在翻动到该小方格上时，骰子朝上的面上所写的字母（字母可“正放”、“横放”或“倒放”）．那么，骰子翻动到画有“﹡”的小方格时，骰子朝上的面所写的字母是（ ）
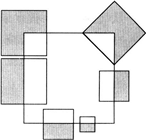（2007?武汉）如图，六个边长为1、2、3的正方形覆盖了一个边长为6的大正方形的一部分，设涂色的部分区域I，大正方形中未被覆盖的部分区域为区域Ⅱ，随机投了一枚硬币，则硬币落在区域I的可能性