题目内容
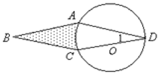 如图,∠1=15°的圆的周长为62.8厘米,点O为圆心,平行四边形的面积为100平方厘米.阴影部分的面积是
如图,∠1=15°的圆的周长为62.8厘米,点O为圆心,平行四边形的面积为100平方厘米.阴影部分的面积是48
| 5 |
| 6 |
48
(平方厘米).| 5 |
| 6 |
分析:观察图形,为组合图形,分别连接OA、AC,并且过A点作CD的垂线交CD于E,这样图形就分割成了规则图形,然后再根据它们之间的关系一步步求出答案.
解答:解:如图,连接OA、AC,过A点作CD的垂线交CD于E,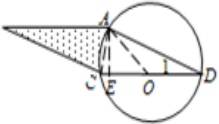 AC是平行四边形的对角线,所以AC分成的两个三角形的面积相等,那么:
AC是平行四边形的对角线,所以AC分成的两个三角形的面积相等,那么:
三角形ACD的面积为100÷2=50(平方厘米),
又圆半径为62.8÷(3.14×2)=10(厘米),因为∠1=15°,
又OA=OD,故∠AOC=15°×2=30°(三角形的外角等于和它不相邻的两个内角和),
扇形AOC的面积为:
×3.14×102=26
(平方厘米),
三角形ACD和三角形ACO高都是AE,由于直径CD是半径OC的2倍,所以三角形AOC的面积是ACD面积的一半;那么:
三角形AOC的面积为:50÷2=25(平方厘米),
小月牙形面积为扇形的面积减去三角形AOC的面积:26
-25=1
(平方厘米),
从而阴影部分的面积为:50-1
=48
(平方厘米).
故答案为:48
.
 AC是平行四边形的对角线,所以AC分成的两个三角形的面积相等,那么:
AC是平行四边形的对角线,所以AC分成的两个三角形的面积相等,那么:三角形ACD的面积为100÷2=50(平方厘米),
又圆半径为62.8÷(3.14×2)=10(厘米),因为∠1=15°,
又OA=OD,故∠AOC=15°×2=30°(三角形的外角等于和它不相邻的两个内角和),
扇形AOC的面积为:
| 30 |
| 360 |
| 1 |
| 6 |
三角形ACD和三角形ACO高都是AE,由于直径CD是半径OC的2倍,所以三角形AOC的面积是ACD面积的一半;那么:
三角形AOC的面积为:50÷2=25(平方厘米),
小月牙形面积为扇形的面积减去三角形AOC的面积:26
| 1 |
| 6 |
| 1 |
| 6 |
从而阴影部分的面积为:50-1
| 1 |
| 6 |
| 5 |
| 6 |
故答案为:48
| 5 |
| 6 |
点评:此题为组合图形的面积,观察图形,恰当加以辅助线,让图形分割成能计算面积的图形,然后逐步计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是学校附近的平面图,请按要求完成以下操作.(测量所得数据取整厘米数)
如图是学校附近的平面图,请按要求完成以下操作.(测量所得数据取整厘米数) 如图为某湖的地图,每一个方块代表1平方千米,那么这个湖的面积大约是( )
如图为某湖的地图,每一个方块代表1平方千米,那么这个湖的面积大约是( )
