题目内容
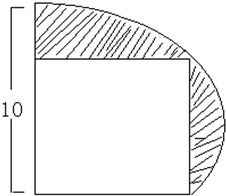 如图
如图| 1 | 4 |
28.5
28.5
平方米.分析:用
圆的面积减正方形的面积就是阴影部分的面积.圆的半径是正方形的对角线,设正方形的边长为a米,根据勾股定理,a2+a2=102,从而求出a2=50,即正方形的面积是50平方米,进而即可求出阴影部分的面积.
| 1 |
| 4 |
解答:解:
圆的面积:
×3.14×102
=
×3.14×100
=78.5(平方米),
正方形的面积:
设正方形的边长为a米,由勾股定理
a2+a2=102
2a2=100
a2=50,
阴影分部的面积:
78.5-50
=28.5(平方米);
故答案为:28.5
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
=78.5(平方米),
正方形的面积:
设正方形的边长为a米,由勾股定理
a2+a2=102
2a2=100
a2=50,
阴影分部的面积:
78.5-50
=28.5(平方米);
故答案为:28.5
点评:此题要求正方形的边长,再求正方形的面积,小学阶段不可以,设出正方形的边长,恰巧得到正方形边长的平方,也就是正方形的面积.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目

 (1)作为上海经济发展的“助推器”和上海中心城区的“辅城”--临港新城,将在南汇崛起.据规划,临港新城总面积达297平方公里,分四个功能区:主城区、主产业区、重装备产业区和物流园区、综合区.部分规划数据见下表.请根据所提供的数据完成下列问题(结果精确到个位).
(1)作为上海经济发展的“助推器”和上海中心城区的“辅城”--临港新城,将在南汇崛起.据规划,临港新城总面积达297平方公里,分四个功能区:主城区、主产业区、重装备产业区和物流园区、综合区.部分规划数据见下表.请根据所提供的数据完成下列问题(结果精确到个位). (1)6时15分=
(1)6时15分= 已知如图中正方形的面积是36cm2,图中
已知如图中正方形的面积是36cm2,图中