题目内容
13.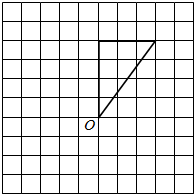 画出正确的图形
画出正确的图形(1)将图形绕O点顺时针旋转90°;
(2)将(1)中所得的图形画出另一半,使它成为一个轴对称图形;
(3)试求(2)中的图形面积(网格是由边长为1的小正方形组成的)
分析 (1)根据旋转的特征,三角形绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同相同方向旋转相同的度数即可画出旋转后的图形.
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,以点O所在纵向直线为对称,在对称轴的左边画出(1)图的关键对称点,依次连结即可.
(3)根据三角形面积计算公式“S=$\frac{1}{2}$ah”即可求出(2)中的图形面积.
解答 解:(1)将图形绕O点顺时针旋转90°(下图):
(2)将(1)中所得的图形画出另一半,使它成为一个轴对称图形(下图):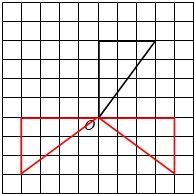
(3)4×2×$\frac{1}{2}$×2
=8×$\frac{1}{2}$×2
=4×2
=8
答:(2)中的图形面积是8.
点评 此题主要是考查作旋转一定度数后的图形、作轴对称图形、三角形面积的计算.

练习册系列答案
相关题目
1.在横线里填上“>”、“<”或“﹦”.
| 150分<3时 | 1千米>999米 | 50厘米<45分米 |
| $\frac{3}{5}$<$\frac{4}{5}$ | $\frac{1}{6}$>$\frac{1}{8}$ | 5千克=5000克 |
3.56×8×0( )56+8+0.
| A. | < | B. | = | C. | > |