题目内容
平面上有100条直线，其中没有两条直线相互平行，也没有三条直线或三条以上直线相交于一点，平面上这100条直线共有交点多少个？
从1条直线开始，找出它们的交点个数的规律特点如下：
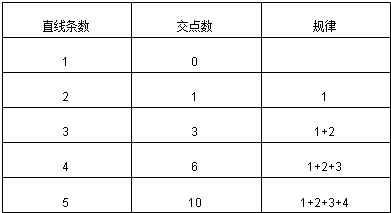
从上面可以看出：当有n条直线时，交点数为：1+2+3+…+（n-1）=
，
所以当有100条直线时，交点数为
=4950，
答：平面上这100条直线共有交点4950个．
从上面可以看出：当有n条直线时，交点数为：1+2+3+…+（n-1）=
| n(n-1) |
| 2 |
所以当有100条直线时，交点数为
| 100×(100-1) |
| 2 |
答：平面上这100条直线共有交点4950个．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
…第78个是（ ）
