题目内容
在1，2，…，1994这1994个数中选出一些数，使得这些数中的每两个数的和都能被26整除，那么这样的数最多能选出
76
76
个．分析：因为26是13的倍数，可以根据能被26和13整除的特征进行解答．
解答：解：有两种选法：
（1）选出所有26的整数倍的数，即：26，26×2，26×3，26×76=1976，共76个数；
（2）选出所有13的奇数倍的数，即：13，13+26×1，13+26×2，13+26×76=1989，共76个数；
答：这样的数最多能选出76个；
故答案为：76．
（1）选出所有26的整数倍的数，即：26，26×2，26×3，26×76=1976，共76个数；
（2）选出所有13的奇数倍的数，即：13，13+26×1，13+26×2，13+26×76=1989，共76个数；
答：这样的数最多能选出76个；
故答案为：76．
点评：此题主要考查整除的意义，根据能被26和13整除的特征解决有关问题．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
：x=2
：1.8
]×（1÷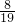
-2.375）]+2.901
和原二班的