题目内容
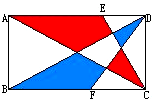（如图）这是一个长方形．| AE |
| ED |
| 9 |
| 5 |
| BF |
| FC |
| 7 |
| 4 |
分析：设长方形的长和宽分别为a和b，分别依据三角形ACE和三角形BDF与长方形的面积的关系，用a、b分别表示出红色部分和蓝色部分的面积，再比较大小即可．
解答：解：设长方形的长和宽分别为a和b，
则三角形ADC的面积为
ab，
三角形AEC的面积为
×
ab=
ab=
ab，
三角形BDF的面积为
×
ab=
ab=
ab，
因为
ab＞
ab，
所以涂红色两块图形的面积大．
则三角形ADC的面积为
| 1 |
| 2 |
三角形AEC的面积为
| 9 |
| 9+5 |
| 1 |
| 2 |
| 9 |
| 28 |
| 99 |
| 308 |
三角形BDF的面积为
| 7 |
| 7+4 |
| 1 |
| 2 |
| 7 |
| 22 |
| 98 |
| 308 |
因为
| 99 |
| 308 |
| 98 |
| 308 |
所以涂红色两块图形的面积大．
点评：解答此题的关键是：用长方形的长和宽分别表示出各自的面积，问题即可得解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2011?青山湖区模拟）如图，这是一个
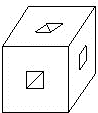在一个棱长为5厘米的正方体木块的各个面中间打一个边长为1厘米的方孔（如图所示）后，这木块的体积是多少立方厘米？