题目内容
 如图,一个边长为50米的正方形围墙,甲乙两人分别从A、C两点同时出发,沿围墙按顺时针方向运动,已知甲每秒走5米,乙每秒走3米,则至少经过
如图,一个边长为50米的正方形围墙,甲乙两人分别从A、C两点同时出发,沿围墙按顺时针方向运动,已知甲每秒走5米,乙每秒走3米,则至少经过30
30
秒甲乙走到正方形的同一条边上.分析:甲在A处,乙在B处,甲乙相距50×2=100(米);当甲从A走到C处,用100÷5=20(秒);那么乙20秒走3×20=60(米),到达D处并超过D处60-50=10(米),走在AD边上;甲从C处到D处用的时间为50÷5=10(秒);那么乙10秒走3×10=30(米);这时乙超过D处10+30=40(米),还在AD边上,甲也在AD边上;所以共用时间10+20=30(秒).
解答:解:①当甲从A走到C处,用的时间:
50×2÷5=20(秒);
②乙20秒走:
3×20=60(米),
这时乙走在AD边上;
③甲从C处到D处用的时间为:
50÷5=10(秒);
这时甲与乙都在AD边上.
④共用时间:
10+20=30(秒).
答:至少经过30秒甲乙走到正方形的同一条边上.
故答案为:30.
50×2÷5=20(秒);
②乙20秒走:
3×20=60(米),
这时乙走在AD边上;
③甲从C处到D处用的时间为:
50÷5=10(秒);
这时甲与乙都在AD边上.
④共用时间:
10+20=30(秒).
答:至少经过30秒甲乙走到正方形的同一条边上.
故答案为:30.
点评:此题属于追及问题,有一定难度.注意本题在解答时,要求甲乙走到正方形的同一条边上,也就是甲刚刚拐弯时就能看到乙.

练习册系列答案
相关题目
 如图,一个正方形,边长增加5米,面积增加125米2,则原来这个正方形的边长为 ( )
如图,一个正方形,边长增加5米,面积增加125米2,则原来这个正方形的边长为 ( ) (2008?宜兴市)如图是一个直角三角形,以长为
(2008?宜兴市)如图是一个直角三角形,以长为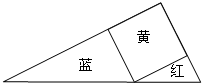 用一张斜边30厘米的红色直角三角形纸片,一张斜边为50厘米的蓝色直角三角形,一张边长为25厘米的黄色的正方形纸片,拼成如图的一个直角三角形.红、蓝两张三角形纸片面积之和是多少平方厘米?
用一张斜边30厘米的红色直角三角形纸片,一张斜边为50厘米的蓝色直角三角形,一张边长为25厘米的黄色的正方形纸片,拼成如图的一个直角三角形.红、蓝两张三角形纸片面积之和是多少平方厘米?