Question

11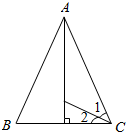．如图，∠1=35°，∠1=∠2，你能用几种方法求出等腰三角形ABC中∠A的度数？

Answer 1

分析 （1）在△ADC中，因为∠1=∠2，可求出∠ACD的度数，进而求出∠3的度数，再根据等腰三角形的性质，求得∠3=∠4，解决问题；

（2）在△ABC中，利用等腰三角形的性质，求得∠B=∠C，再根据三角形内角和定理，求得∠A的度数即可．

解答 解：（1）在△ADC中，因为∠1=∠2，
所以∠3=180-90°-∠ACD=90°-35°×2=20°；
在等腰△ABC中，因为AB=AC，AD⊥BC，所以∠3=∠4=20°，
所以∠BAC=∠3+∠4=20°+20°=40°．

（2）在△ABC中，
因为AB=AC，
所以∠B=∠C，
因为∠C=∠1+∠2=35°+35°=70°，
所以∠B=70°，
所以∠A=180°-∠B-∠C=180°-70°-70°=40°．

点评 此题考查了等腰三角形的性质以及三角形内角和定理．运用它们解决问题．