题目内容
如图所示，四边形ABCD与四边形CPMN都是平行四边形，若三角形DFP与三角形AEF的面积分别是22和36，则三角形BNE的面积为分析：如下图所示，连接AM，由等底等高的三角形的面积相等，有S△DAP=S△DAM，所以S△DAP-S△DAF=S△DAM-S△DAF，即S△PDF=S△MAF=22，同理可得，S△BNE=S△MAE，
所以S△BNE=S△MAE=S△EAF-S△MAF=36-22=14，据此解决即可．
所以S△BNE=S△MAE=S△EAF-S△MAF=36-22=14，据此解决即可．
解答：解：如上图所示：因为S△DAP=S△DAM，
所以S△DAP-S△DAF=S△DAM-S△DAF，
即S△PDF=S△MAF=22．
同理可得，S△BNE=S△MAE，
所以S△BNE=S△MAE=S△EAF-S△MAF=36-22=14．
答：三角形BNE的面积为14．
故答案为：14．
所以S△DAP-S△DAF=S△DAM-S△DAF，
即S△PDF=S△MAF=22．
同理可得，S△BNE=S△MAE，
所以S△BNE=S△MAE=S△EAF-S△MAF=36-22=14．
答：三角形BNE的面积为14．
故答案为：14．
点评：本题解决的关键是能作出辅助线，利用等底等高的三角形的面积相等解决．
练习册系列答案
相关题目
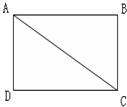如图所示，四边形ABCD是一个长为4，宽为3，对角线长度为5的长方形．它绕C点接顺时针方向旋转90度，请求出AB边扫过图形的面积．
分别延长四边形ABCD的四个边，使得AB=BA′，BC=CB′，CD=DC′，DA=AD′（如图所示）．如果四边形ABCD的面积是1平方公分，试求四边形A′B′C′D′的面积？
如图所示，正方形ABCD的边长为10厘米，E、F分别为AB 及BC的中点．四边形BFGE的面积是
如图所示的四边形ABCD中，∠A=∠C=45°，∠ABC=105°，AB=CD=15厘米，连接对角线BD．求四边形ABCD的面积．
如图所示，四边形ABCD是一个长为4，宽为3，对角线长度为5的长方形．它绕C点接顺时针方向旋转90度，请求出AB边扫过图形的面积．