题目内容
将1，2，3，…，2000，2001，2002这2002个数从小到大排成一列．算出前999个数的平均数及后面1003个数的平均数，这两个平均数的差是 ．
分析：前999个数额平均数是（999+1）÷2=500，后面1003个数的平均数是：（1000+2002）÷2=1501，据此相减即可解答问题．
解答：解：（1000+2002）÷2-（999+1）÷2
=3002÷2-1000÷2
=1501-500
=1001；
答：这两个平均数的差是1001．
故答案为：1001．
=3002÷2-1000÷2
=1501-500
=1001；
答：这两个平均数的差是1001．
故答案为：1001．
点评：将1，2，3，…，2000，2001，2002这2002个数从小到大排成一列．后面1003个数的平均数等于1000到2002最中间的数字；前999个数的平均数，等于1到999最中间的数字，据此即可解答．
练习册系列答案
相关题目
（2012?淮安模拟）（1）看图，图中三角形三个顶点A、B、C的位置是A（ 1、2 ） B（3、2 ） C（1、5 ），请在三个顶点上标出字母．
将1，2，3，4分别填入4×4的方格网（如图所示）的16个小方格中，使得每一行每一列中的4个数1，2，3，4恰好各出现一次，并且满足与不等号相邻的两个数中小数是大数的约数，那么，从左上到右下的对角线上4个数的和是（ ）（左图是一个3×3的例子）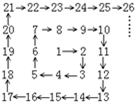
将自然数1，2，3，4…按箭头所指方向顺序排列（如图），依次在2，3，5，7，10…等数的位置处拐弯．