题目内容
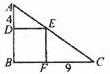 图中ABC是直角三角形,BDEF是正方形,AD=4厘米,FC=9厘米,则ABC的面积=
图中ABC是直角三角形,BDEF是正方形,AD=4厘米,FC=9厘米,则ABC的面积=75
75
平方厘米.分析:由图意可知:S△ABC=S△ADE+S正方形BDEF+S△EFC,设正方形的边长为a,再据题目所给数据,代入此等式,即可求出a的值,进而求出三角形ABC的面积.
解答:解:设正方形的边长为a,
则S△ABC=S△ADE+S正方形BDEF+S△EFC,
即
×(9+a)×(4+a)=
×4×a+a2+
×9a,
a2+
a+2a+18=2a+
a+a2,
a2+18=a2,
a2=18,
a2=36;
所以a=6(厘米);
所以三角形ABC的面积为:
×(9+6)×(4+6),
=
×15×10,
=75(平方厘米);
答:三角形ABC的面积是75平方厘米.
故答案为:75.
则S△ABC=S△ADE+S正方形BDEF+S△EFC,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
a2=36;
所以a=6(厘米);
所以三角形ABC的面积为:
| 1 |
| 2 |
=
| 1 |
| 2 |
=75(平方厘米);
答:三角形ABC的面积是75平方厘米.
故答案为:75.
点评:解答此题的关键是:找出等量关系S△ABC=S△AFB+S正方形FBDE+S△EDC,即可列方程求解.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
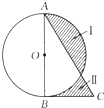 如图,△ABC是直角三角形,AB为圆直径,AB=20,阴影I的面积比阴影Ⅱ的面积大7,求BC的长.
如图,△ABC是直角三角形,AB为圆直径,AB=20,阴影I的面积比阴影Ⅱ的面积大7,求BC的长.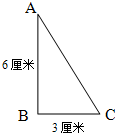 如图,ABC是直角三角形,以AB为轴并将三角形绕这个轴旋转一周得到一个旋转体,求这个旋转体的体积.
如图,ABC是直角三角形,以AB为轴并将三角形绕这个轴旋转一周得到一个旋转体,求这个旋转体的体积. 图中ABC是直角三角形,BDEF是正方形,AD=4厘米,FC=9厘米,则ABC的面积=________平方厘米.
图中ABC是直角三角形,BDEF是正方形,AD=4厘米,FC=9厘米,则ABC的面积=________平方厘米. 如图,△ABC是直角三角形,AB为圆直径,AB=20,阴影I的面积比阴影Ⅱ的面积大7,求BC的长.
如图,△ABC是直角三角形,AB为圆直径,AB=20,阴影I的面积比阴影Ⅱ的面积大7,求BC的长.