题目内容
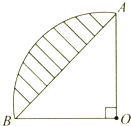 图中已知AB的长8厘米,求阴影部分的面积是多少平方厘米?
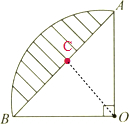
图中已知AB的长8厘米,求阴影部分的面积是多少平方厘米?分析:图中阴影部分的面积等于扇形的面积减去△AOB的面积,如下图所示,设AB的中点为点C,连接OC,则线段OC即为直角三角形AOB的斜边AB上的高,且OC=
AB=
×8,由三角形的面积公式可求得△AOB的面积,设扇形的半径为r厘米,则OA=OB=r,由△AOB的面积还可以表示为
×OA×OB=
r2,则可求得r2的值,进而求得扇形的面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

解答:解:设扇形的半径为r厘米,则OA=OB=r,
由分析可知,△AOB的面积是:8×(
×8)÷2,
=8×4÷2,
=16(平方厘米),
所以
×OA×OB=
r2=16,
r2=32,
扇形的面积是
πr2=
×3.14×32=25.12(平方厘米),
所以阴影部分的面积是:25.12-16=9.12(平方厘米).
答:阴影部分的面积是9.12平方厘米.
由分析可知,△AOB的面积是:8×(
| 1 |
| 2 |
=8×4÷2,
=16(平方厘米),
所以
| 1 |
| 2 |
| 1 |
| 2 |
r2=32,
扇形的面积是
| 1 |
| 4 |
| 1 |
| 4 |
所以阴影部分的面积是:25.12-16=9.12(平方厘米).
答:阴影部分的面积是9.12平方厘米.
点评:本题考查组合图形的面积,解决问题的关键是求出三角形和扇形的面积.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为
如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 图中已知长方形ABCD长60厘米,宽40厘米,M为CD中点,点P由C移动到B时,三角形AMP的面积增加了
图中已知长方形ABCD长60厘米,宽40厘米,M为CD中点,点P由C移动到B时,三角形AMP的面积增加了 如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为________平方厘米.
如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为________平方厘米.