Question

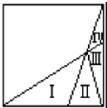在正方形里面画出四个小三角形（如图），
三角形Ⅰ与Ⅱ的面积之比是2：1；三角形Ⅲ与Ⅳ的面积相等；三角形Ⅰ、Ⅱ、Ⅲ的面积之和是

1

4

平方米；三角形Ⅱ、Ⅲ、Ⅳ的面积之和是

1

6

平方米；那么这四个小三角形的面积总和是

3

10

平方米．

Answer 1

分析：设三角形Ⅰ，Ⅱ，Ⅲ，Ⅳ的面积分别为a，b，c，d；依据题目得 a=2b，c=d；a+b+c=

1

4

；b+c+d=

1

6

；由此进行代换求解．

解答：解：设三角形Ⅰ，Ⅱ，Ⅲ，Ⅳ的面积分别为a，b，c，d；依据题目得：
a=2b，c=d；
a+b+c=

1

4

；①
b+c+d=

1

6

；②
①可以化简为：
3b+c=

1

4

，
c=

1

4

-3b；
②可以化简为：
b+2c=

1

6

，③
把c=

1

4

-3b代入③可得：
b+2×（

1

4

-3b）=

1

6

，
       b+

1

2

-6b=

1

6

，
            5b=

1

2

-

1

6

，
            5b=

1

3

，
             b=

1

15

；
c=

1

4

-3×

1

15

=

1

20

；
a+b+c+d，
=3b+2c，
=3×

1

15

+2×

1

20

，
=

1

5

+

1

10

，
=

3

10

（平方米）；
答：这四个小三角形的面积总和是

3

10

平方米．
故答案为：

3

10

．

点评：本题先根据给出的已知条件找出等量关系，写出等式，然后把等式通过加减或代换变成只含有一个未知数的方程，解方程求解即可．