题目内容
 在平行四边形ABCD中,E、F分别是BD、CD的中点.已知三角形AEF的面积是30平方厘米,求平行四边形ABCD的面积.
在平行四边形ABCD中,E、F分别是BD、CD的中点.已知三角形AEF的面积是30平方厘米,求平行四边形ABCD的面积.分析:连接AD,BC,AC如图

EF是三角形BCD的中位线,所以三角形EFD的面积是平行四边形ABCD总面积
,
又因为E、F分别是中点,由三角形的中线可得四边形AEDF是平行四边形ABCD总面积的
,
设总面积为“1”,可得总面积的(
-
)=30,由此列式解答.就可算出平行四边形ABCD的面积.

EF是三角形BCD的中位线,所以三角形EFD的面积是平行四边形ABCD总面积
| 1 |
| 8 |
又因为E、F分别是中点,由三角形的中线可得四边形AEDF是平行四边形ABCD总面积的
| 1 |
| 2 |
设总面积为“1”,可得总面积的(
| 1 |
| 2 |
| 1 |
| 8 |
解答:解:根据分析,设总面积为“1”,
30÷(
-
),
=30÷
,
=30×
,
=80(平方厘米);
答:平行四边形ABCD的面积是80平方厘米.
30÷(
| 1 |
| 2 |
| 1 |
| 8 |
=30÷
| 3 |
| 8 |
=30×
| 8 |
| 3 |
=80(平方厘米);
答:平行四边形ABCD的面积是80平方厘米.
点评:此题主要根据等底等高的三角形的面积相等,通过作辅助线,求出三角形的面积占总面积的几分之几,再根据已知一个数的几分之几是多少,求这个数,用除法解答.

练习册系列答案
相关题目
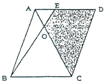 如右图,在平行四边形ABCD中OE:0B=1:3,三角形AOB的面积是30平方厘米.求阴影部分的面积是多少平方厘米.
如右图,在平行四边形ABCD中OE:0B=1:3,三角形AOB的面积是30平方厘米.求阴影部分的面积是多少平方厘米. 在平行四边形ABCD中,已知∠A=70°,求其他3个角的度数.∠A=70°∠B=
在平行四边形ABCD中,已知∠A=70°,求其他3个角的度数.∠A=70°∠B= (2010?深圳模拟)如图,在平行四边形ABCD中,AE=
(2010?深圳模拟)如图,在平行四边形ABCD中,AE= 如图,在平行四边形ABCD中,BE交AC于点F,交CD于点E,己知三角形BCF的面积是15平方厘米,三角形CEF的面积是10平方厘米.那么,四边形ADEF的面积是
如图,在平行四边形ABCD中,BE交AC于点F,交CD于点E,己知三角形BCF的面积是15平方厘米,三角形CEF的面积是10平方厘米.那么,四边形ADEF的面积是