题目内容
求1,2,3,4,…,1 997,1 998,1 999这些自然数中所出现的所有数字之和.
答案:
解析:
解析:
|
求这些自然数中所出现的所有数字之和,不能用将数字1、2、3、4、5、6、7、8、9、0分类的方法,因为分类后也很麻烦,我们可以用分组的方法,每组两个数,若这两个数相加不进位,即可求这个和的各位数字之和代替原来两个数各位数字之和,若所分的各组中两个数的和都相同,就比较容易得出结果. 将0至1 999的整数分组: (0,1 999),(1,1 998),(2,1 997),(3,1 996),…,(998,1 001),(999,1 000). 每组两数之和为1 999,共有1 000组,并且每一组两数相加都不进位,这样,1到1 999的所有数字之和就等于: (1+9+9+9)×1 000=28 000. 因此,从1到1 999的所有数字之和为28 000. |

练习册系列答案
相关题目
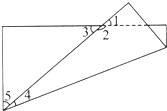 把一张长方形纸折成如图的形状,已知∠1+∠2+∠3=220°,∠4=20°,求∠1、∠2、∠3、∠5各是多少度.
把一张长方形纸折成如图的形状,已知∠1+∠2+∠3=220°,∠4=20°,求∠1、∠2、∠3、∠5各是多少度. 求角的度数.(如图)∠1=35°∠2=
求角的度数.(如图)∠1=35°∠2=