题目内容
9.如图,边长为20cm和30cm的两个正方形拼放在一起,求△ABC的面积?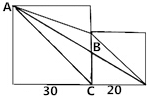
分析 如图: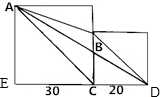
根据图意,两个正方形拼放在一起,因为BC∥AE,所以△CBD和△AED相似,因为CD=20厘米,AE=30厘米,即BC:AE=CD:CE=20:(20+30),由此即可求得BC的长度,再根据三角形的面积公式:s=ah÷2,即可求出阴影部分的面积.
解答 解:如上图:
因为BC∥AE,
所以△BCD和△AED相似,
因为CD=20厘米,AE=30厘米,
即BC:AE=CD:CE=20:(20+30),
所以,BC:AE=20:50,
即BC:30=20:50,
BC=$\frac{30×20}{50}$
=12(厘米),
12×30÷2
=360÷2
=180(平方厘米),
答:三角形ABC的面积是180平方厘米.
点评 此题考查了相似三角形的对应边成比例的性质及三角形的面积公式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.直接写得数
| 0.32×5= | 4.8÷0.6= | 0.72÷0.1= |
| 12.5×8= | 1.2÷24= | 2.5×8= |
18.甲数是乙数的$\frac{1}{2}$,甲数与乙数( )
| A. | 成正比例 | B. | 不成正比例 | C. | 不是相关联的量 |
