Question

如图，正方形ABCD被分成了面积相同的8个三角形，如果DG=5，那么正方形ABCD面积是

64

．

Answer 1

分析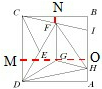：如图，过G点做MO平行AD，交CD、AB分别于点M、O，过点F做FN⊥BC于N．设正方形面积为“1”，则正方形边长为1，根据正方形ABCD被分成了面积相同的8个三角形，可求出BI、HA的长度，再根据四边形FGHI是平行四边形，求出FG、GO、GM的长度，在直角三角形GMD中，根据勾股定理求出DG的长度，最后根据如果DG=5，求出正方形的边长，最后算出面积．

解答：解：如图，过G点做MO平行AD，交CD、AB分别于点M、O，过点F做FN⊥BC于N．
设正方形面积为“1”，则正方形边长为1，图中每个小三角形的面积都是

1

8

，
所以BI=HA=

1

4

，
又因为四边形FGHI是平行四边形，所以HI=FG=

1

2

，GO=GM=

1

2

，FN=

1

8

，
在直角三角形GMD中，MG=

1

2

，MD5=1-

1

8

-

1

2

=

3

8

，
根据勾股定理DG=

1 2 × 1 2 + 3 8 × 3 8

=

5

8

，
所以正方形的边长是5÷

5

8

=8，正方形面积=8×8=64．
故答案为：64．

点评：本题难度较大，解题关键是作辅助线求出正方形的边长．