题目内容
6.如图,以一个直角三角形ABC的一直角边为直径作半圆,P是半圆弧的最高点,连结BP,已知阴影部分的面积与空白部分面积的差为16,若在该半圆内作一个最大的圆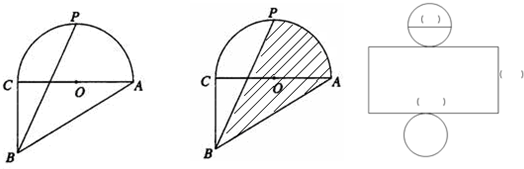
(1)求该圆的直径;
(2)以与该圆面积相等的圆为底作一个圆柱,圆柱的展开图如图所示,图中长方形的长与宽之比为3.14:1.请在图中括号内标明相应的数据;
(3)计算该圆柱的体积.
分析 (1)利用圆的对称性可知:两个阴影部分面积相等(OC=OA;CD=EA;OD=OE)
等底同高的三角形面积相等 所以 S△POD=S△POE;S△CDB=S△AEB;S△BOD=S△BOE;
于是:S△BOP=S△POD+S△BOD=S△POE+S△BOE,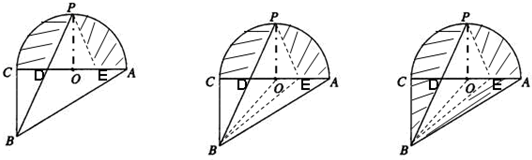
根据题意阴影部分的面积与空白部分面积的差为16,即为三角形PEB的面积是16,据此解答即可.
(2)根据第一问求得的数据可知,d=4,c=长方形的长=πd=3.14×4=12.56,再根据长方形的长与宽之比为3.14:1求得长方形的宽是12.56÷3.14=4.
(3)根据圆柱的体积V=sh解答即可.
解答 解:如图,利用圆的对称性可知:两个阴影部分面积相等(OC=OA;CD=EA;OD=OE)
等底同高的三角形面积相等 所以 S△POD=S△POE;S△CDB=S△AEB;S△BOD=S△BOE;
于是:S△BOP=S△POD+S△BOD=S△POE+S△BOE
因此 原图中阴影部分与空白部分的面积差就转化为三角形PBE的面积了,
则有:2S△BOP=16
所以:
$2×\frac{1}{2}OP•OC=16$
OP=OC=4
即小圆的直径为4.
(2)3.14×4=12.56
12.56÷3.14=4
答:小圆直径处填4,长方形的长是12.56,长方形的宽是4.
故答案为:4,12.56,4.
(3)3.14×(4÷2)2×4
=3.14×16
=50.24
答:圆柱的体积是50.24.
点评 解决此题的关键是做出合适的辅助线,将图形进行相应转换,利用已知条件求得阴影部分的面积.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
17.快乐口算.
| 25×4= | 240×3= | 160×5= |
| 60×120= | 180÷30= | 360÷6= |
14.在一个比例尺是20:1的图纸上,量得一个零件的长是2厘米,这个零件实际长( )
| A. | 4分米 | B. | 0.1厘米 | C. | 1分米 | D. | 0.4厘米 |
11.889÷9商的最高位是( )
| A. | 个位 | B. | 十位 | C. | 百位 |
15. 从正面看到的形状是( )
从正面看到的形状是( )
 从正面看到的形状是( )
从正面看到的形状是( )| A. |  | B. |  | C. |  |
