题目内容
8.一项工作,甲乙两人合作12天完成,现在先由甲独做2天,再由乙独做5天,两人完成了这项工程的$\frac{1}{4}$,假如这项工程由乙单独完成,共需多少天?分析 甲乙两队合做12天可以完成,求出甲乙的工作效率之和$\frac{1}{12}$;甲队做2天,乙队做5天,相当于甲乙合作2天,乙再单独做5-2=3天,正好完成这项工程的$\frac{1}{4}$,根据工作量=工作效率×工作时间,求出甲乙合作2天的工作量,进而求出乙单独做3天的工作量,以及乙的工作效率,进一步求得由乙队单独完成,一共需要多少天即可.
解答 解:1÷[($\frac{1}{4}$-$\frac{1}{12}$×2)÷(5-2)]
=1÷[$\frac{1}{12}$÷3]
=1÷$\frac{1}{36}$
=36(天)
答:这项工程由乙单独完成,共需36天.
点评 本题考查了工作时间、工作量、工作效率三者之间的关系.解答本题的关键是先求出乙的工作效率.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
3.一个不等于0的数除以假分数,所得的商( )这个数.
| A. | 大于 | B. | 小于 | C. | 等于 | D. | 大于或等于 | ||||
| E. | 都不是 |

 ,从正面看到的形是
,从正面看到的形是 ,从左面看到的形状是
,从左面看到的形状是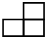 ,这是由( )个小正方体搭成的立体图形.
,这是由( )个小正方体搭成的立体图形.