Question

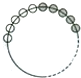如图，沿着圆周放置黑、白棋子各100枚，并且各自相邻排列．若将圆周上任意两枚棋子换位一次称为一次对换，则至少经过

50

次对换可使全部的黑棋子彼此不相邻．

Answer 1

分析：从黑白珠子相交的地方为起点，黒棋子和白棋子的第一个都不用动，第二个交换位置；第三个不动，第四个交换位置，…只要交换位置为偶数的棋子的位置即可．

解答：解：从黑白珠子相交的地方为起点，分别数白棋子和黑棋子，只要交换偶数位置的棋子就可以；这样就需要交换：
100÷2=50（次）；
故答案为：50．

点评：此题是考察学生观察、发现、归纳规律解决问题的能力．要求学生利用归纳规律解答问题．