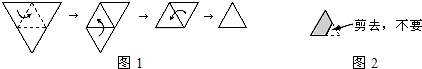题目内容
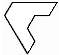
将图1中的三角形纸片沿虚线折叠得到图2,其中的粗实线图形面积与原三角形面积之比为2:3.已知图2中3个画阴影的三角形面积之和为1,那么重叠部分的面积为多少?


分析:如图,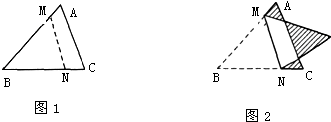
三角形ABC的面积为三角形BMN与四边形AMNC的和,即为2倍的重叠部分的面积与阴影面积的和,而粗边面积为重叠的面积与阴影面积的和;假设重叠部分的面积为x,然后根据“粗实线图形面积与原三角形面积之比为2:3”和已知阴影的三角形面积之和为1,列出等式:(x+1):(2x+1)=2:3,根据比例的性质“两外项之积等于两内项之积”得到方程,解方程即可得解.

三角形ABC的面积为三角形BMN与四边形AMNC的和,即为2倍的重叠部分的面积与阴影面积的和,而粗边面积为重叠的面积与阴影面积的和;假设重叠部分的面积为x,然后根据“粗实线图形面积与原三角形面积之比为2:3”和已知阴影的三角形面积之和为1,列出等式:(x+1):(2x+1)=2:3,根据比例的性质“两外项之积等于两内项之积”得到方程,解方程即可得解.
解答:解:设重叠部分的面积为x,
则三角形ABC的面积为:2×x+1=2x+1,
粗边围成的面积为:x+1,
因为粗实线图形面积与原三角形面积之比为2:3,
所以:(x+1):(2x+1)=2:3,
4x+2=3x+3,
4x-3x=3-2,
x=1;
所以重叠部分的面积为1.
则三角形ABC的面积为:2×x+1=2x+1,
粗边围成的面积为:x+1,
因为粗实线图形面积与原三角形面积之比为2:3,
所以:(x+1):(2x+1)=2:3,
4x+2=3x+3,
4x-3x=3-2,
x=1;
所以重叠部分的面积为1.
点评:本题考查了折叠面积的性质,折叠的图形和折叠后的图形对应相等.

练习册系列答案
相关题目
 将如图(1)所示的三角形纸片沿粗虚线折叠成如图(2)所示的图形.已知图(1)三角形的面积是图(2)图形面表的1.5倍,图(2)中阴影部分的面积之和为1平方厘米.求重叠部分的面积.
将如图(1)所示的三角形纸片沿粗虚线折叠成如图(2)所示的图形.已知图(1)三角形的面积是图(2)图形面表的1.5倍,图(2)中阴影部分的面积之和为1平方厘米.求重叠部分的面积.