题目内容
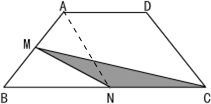
 在面积为1的梯形ABCD中,M、N分别为AB、BC的中点,AD=BN,求阴影部分的面积.
在面积为1的梯形ABCD中,M、N分别为AB、BC的中点,AD=BN,求阴影部分的面积.分析:连接AN,则梯形的面积就分成了两部分:三角形ABN的面积和平行四边形ADCN的面积,因为AD=BN=NC,根据梯形与三角形的面积公式可得:三角形ABN的面积=
平行四边形ADCN的面积=
梯形的面积=1×
=
;因为N是BC的中点,所以三角形BMN与三角形MNC的面积相等,同理,因为M是AB的中点,则三角形BMN的面积=
三角形ABN的面积,由此即可解答问题.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |

解答:解:连接AN,因为AD=BN=NC,不难得出:三角形ABN的面积=
平行四边形ADCN的面积=
梯形的面积=1×
=
;
因为N是BC的中点,所以三角形BMN与三角形MNC的面积相等,
因为M是AB的中点,
则三角形MNC的面积=三角形BMN的面积=
三角形ABN的面积=
×
=
,
答:阴影部分的面积是
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
因为N是BC的中点,所以三角形BMN与三角形MNC的面积相等,
因为M是AB的中点,
则三角形MNC的面积=三角形BMN的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
答:阴影部分的面积是
| 1 |
| 6 |
点评:连接AN,把梯形划分成,等底等高的三角形和平行四边形,从而得出三角形的面积是梯形的面积的
,再利用高一定时,三角形的面积与底成正比例的性质,即可解决问题.
| 1 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



 ,△ADE的面积是梯形ABCD面积的
,△ADE的面积是梯形ABCD面积的 ,求阴影部分面积.
,求阴影部分面积.