题目内容
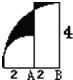 如图,A、B是两个圆(只有
如图,A、B是两个圆(只有| 1 | 4 |
1.42
1.42
.(π=3.14)
分析:设长方形图中空白部分的面积为a,因此图中大阴影部分的面积就等于半径为4的大扇形的面积减去半径为2的小扇形的面积再减去a,即
×3.14×42-
×3.14×22-a;小阴影的面积等于长方形的面积减去a,即2×4-a,两式相减即可求解.
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(
×3.14×42-
×3.14×22-a)-(2×4-a)
=(12.56-3.14-a)-(8-a)
=(9.42-a)-(8-a)
=9.42-8
=1.42;
答:两个阴影部分的面积差是1.42.
故答案为:1.42.
| 1 |
| 4 |
| 1 |
| 4 |
=(12.56-3.14-a)-(8-a)
=(9.42-a)-(8-a)
=9.42-8
=1.42;
答:两个阴影部分的面积差是1.42.
故答案为:1.42.
点评:本题解决的关键是设长方形图中空白部分的面积为a,分别表示出两个阴影部分的面积.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 如图,A、B是两个圆(只画出圆
如图,A、B是两个圆(只画出圆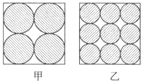 如图,甲和乙是两个面积相等的正方形,甲中阴影部分是4个圆,乙中阴影部分是9个圆,甲和乙中阴影部分的面积比较,( )
如图,甲和乙是两个面积相等的正方形,甲中阴影部分是4个圆,乙中阴影部分是9个圆,甲和乙中阴影部分的面积比较,( ) 仔细观察如图1所示的两个圆,并回答问题.
仔细观察如图1所示的两个圆,并回答问题.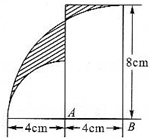 如图,A、B是两个圆(只画出圆
如图,A、B是两个圆(只画出圆 )的圆心,那么,两个阴影部分的面积差是多少?(π取3.14)
)的圆心,那么,两个阴影部分的面积差是多少?(π取3.14)