题目内容
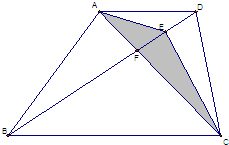如图所示，ABCD是梯形，三角形ADE的面积为1，三角形ABF的面积为9，三角形BCF的面积为27，则三角形ACE的面积为8
8
．分析：（1）三角形ABF的面积为9，三角形BCF的面积为27，根据高一定时，三角形的面积与底成正比例的性质可得：AF：FC=9：27=1：3，梯形ABCD中，三角形ADF与三角形BFC相似，相似比是AF：FC=1：3，则它们的面积之比等于相似比的平方：1：9，所以三角形ADF的面积是：27÷9=3；
（2）又因为三角形ADE的面积是1，所以三角形AEF的面积是2，根据高一定时，三角形的面积与底成正比例的性质，再求出三角形EFC的面积即可解决问题．
（2）又因为三角形ADE的面积是1，所以三角形AEF的面积是2，根据高一定时，三角形的面积与底成正比例的性质，再求出三角形EFC的面积即可解决问题．
解答：解：由SABF=9，SBCF=27，可得AF：FC=1：3，
则 SADF：SBCF=1：9，
∴SADF=1×27÷9=3，
又∵SADE=1，
∴SAEF=2，
∴SEFC=6，
∴SAEC=2+6=8．
答：三角形AEC的面积是8．
故答案为：8．
则 SADF：SBCF=1：9，
∴SADF=1×27÷9=3，
又∵SADE=1，
∴SAEF=2，
∴SEFC=6，
∴SAEC=2+6=8．
答：三角形AEC的面积是8．
故答案为：8．
点评：此题考查了相似三角形的面积比等于相似比的平方的性质和高一定时，三角形的面积与底成正比的关系的灵活应用．
练习册系列答案
阅读快车系列答案
相关题目
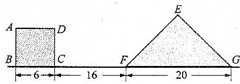如图所示正方形ABCD与1个等腰直角三角形EFG（EF=EG），放在同一直线上．现在三角形不动，正方形以每秒2厘米的速度向右沿直线匀速运动．试回答以下情况时，正方形与三角形重叠部分的面积是多少？
在图中，ABCD是长方形，三条线段的长度如图所示，M是线段DE的中点，求四边形ABMD（阴影部分）的面积（单位：厘米）．
如图所示四边形ABCD是平行四边形，求出梯形与三角形的面积．（单位：cm）
如图所示，P是长方形ABCD内一点，连接PA、PB、PC、PD，长方形被分成甲、乙、丙、丁四个三角形，已知甲的面积占长方形面积的15%，比丙的面积少30平方厘米，长方形ABCD的面积是多少平方厘米？