题目内容
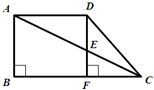 直角梯形ABCD,DF垂直于BC,AD是7.5cm,EF是2.4cm,CF是5cm,那么三角形CDE的面积是
直角梯形ABCD,DF垂直于BC,AD是7.5cm,EF是2.4cm,CF是5cm,那么三角形CDE的面积是分析:连接AF,则三角形ADF和三角形ADC等底等高,则三角形ADF的面积=三角形ADC的面积,两边同时减去三角形DEA的面积,则三角形AEF的面积=三角形DEC的面积,然后根据:三角形的面积=底×高÷2,求出三角形AEF的面积,即求出了三角形CDE的面积.
解答:解: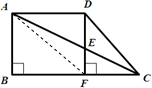
连接AF,则三角形ADF和三角形ADC等底等高,则三角形ADF的面积=三角形ADC的面积,两边同时减去三角形DEA的面积,则三角形AEF的面积=三角形DEC的面积,
则三角形CDE的面积=三角形AEF的面积=2.4×7.5÷2=9(平方厘米);
答:三角形CDE的面积是9平方厘米;
故答案为:9.

连接AF,则三角形ADF和三角形ADC等底等高,则三角形ADF的面积=三角形ADC的面积,两边同时减去三角形DEA的面积,则三角形AEF的面积=三角形DEC的面积,
则三角形CDE的面积=三角形AEF的面积=2.4×7.5÷2=9(平方厘米);
答:三角形CDE的面积是9平方厘米;
故答案为:9.
点评:根据题意你,推导出三角形AEF的面积=三角形DEC的面积,是解答此题的关键.

练习册系列答案
相关题目

 如图所示,长方形ABCD长是6.5厘米,宽是2厘米,过D点作一条线段把长方形分成两部分,一部分是直角三角形,另一部分是梯形.直角三角形与梯形的面积比是1:3,那么直角三角形与梯形的周长相差
如图所示,长方形ABCD长是6.5厘米,宽是2厘米,过D点作一条线段把长方形分成两部分,一部分是直角三角形,另一部分是梯形.直角三角形与梯形的面积比是1:3,那么直角三角形与梯形的周长相差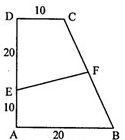 如图,四边形ABCD是直角梯形,∠A=∠D=90?,点E将DA分成2:1,F为BC中点,则四边形FEAB的面积为
如图,四边形ABCD是直角梯形,∠A=∠D=90?,点E将DA分成2:1,F为BC中点,则四边形FEAB的面积为 如图所示,长方形ABCD长是6.5厘米,宽是2厘米,过D点作一条线段把长方形分成两部分,一部分是直角三角形,另一部分是梯形.直角三角形与梯形的面积比是1:3,那么直角三角形与梯形的周长相差________厘米.
如图所示,长方形ABCD长是6.5厘米,宽是2厘米,过D点作一条线段把长方形分成两部分,一部分是直角三角形,另一部分是梯形.直角三角形与梯形的面积比是1:3,那么直角三角形与梯形的周长相差________厘米.