题目内容
3．图中，三角形ABC的面积是30平方分米，BC=12分米，BD=4分米，求空白部分的面积．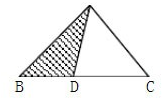
分析 先求出DC的长度，然后根据等高的两个小三角形的底边比即两个小三角形的面积比，已知两个小三角形的面积和是30平方分米，然后运用按比例分配知识进行解答即可．
解答 解：因为BC=12分米，BD=4分米，则CD=12-4=8（分米）
则三角形ABD的面积：三角形ACD的面积=4：8=1：2，
所以三角形ACD的面积=三角形ABC的面积×$\frac{2}{1+2}$=30×$\frac{2}{3}$=20（平方分米）
答：空白部分的面积是20平方分米．
点评 此题考查了组合图形的面积，明确等高的两个三角形的底边比即两个三角形的面积比，是解答此题的关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
8．妈妈把8000元钱存入银行，定期2年，若年利率为4.68%，到期时，她可取回多少利息？正确列式是（ ）
| A． | 8000×4.68%×2+8000 | B． | 8000×4.68%-8000 | ||
| C． | 8000×4.68%×2 | D． | 8000×4.68%+8000 |
王大伯卖出两桶单价相同的苹果（如图），两桶苹果所卖的钱差21.6元．平均每千克苹果的价钱是多少元？