题目内容
ABCD是边长为10厘米的正方形，BG比AG的一半多1厘米．求梯形AEFG的面积．
解：设AG的长为x厘米，
则x+
+1=10，
x=9，
x=6；
S△ADG=
×10×6=30（平方厘米）；
SAEFG=S□AEFD-S△ADG=SABCD-S△ADG=100-30=70（cm2）．
答：梯形AEFG的面积．
分析：由题目条件可以先求出AG的大小，即：AG=（10-l）÷（2+l）=3，从而可以求出三角形ADG的面积；因为梯形AEFG的面积=四边形AEFD的面积-三角形ADG的面积，而四边形AEFD的面积=正方形ABCD的面积，正方形的面积已知，所以就可求出梯形AEFG的面积．
点评：解决此题的关键是先求出先求出AG的大小，再利用等积转换，即可求得梯形的面积．
则x+
+1=10，x=9，x=6；
S△ADG=
×10×6=30（平方厘米）；SAEFG=S□AEFD-S△ADG=SABCD-S△ADG=100-30=70（cm2）．
答：梯形AEFG的面积．
分析：由题目条件可以先求出AG的大小，即：AG=（10-l）÷（2+l）=3，从而可以求出三角形ADG的面积；因为梯形AEFG的面积=四边形AEFD的面积-三角形ADG的面积，而四边形AEFD的面积=正方形ABCD的面积，正方形的面积已知，所以就可求出梯形AEFG的面积．
点评：解决此题的关键是先求出先求出AG的大小，再利用等积转换，即可求得梯形的面积．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
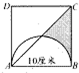
如图，ABCD是边长为10米的正方形，甲从A、乙从D同时开始按逆时针方向沿着正方形的边行走，甲的速度是乙速度的4倍，当甲、乙两人第一次距离（直线距离）最远时，甲行走的路程是
ABCD是边长为10厘米的正方形，BG比AG的一半多1厘米．求梯形AEFG的面积．