题目内容
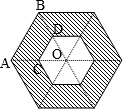
 图中对同一个正六边形,进行了不同的划分,其中小正六边形边长均为是大六边形边长的一半,已知两个图中的阴影部分相差36平方厘米,那么原正六边形面积为
图中对同一个正六边形,进行了不同的划分,其中小正六边形边长均为是大六边形边长的一半,已知两个图中的阴影部分相差36平方厘米,那么原正六边形面积为48
48
平方厘米.分析:如图:因为小正六边形边长均为是大六边形边长的一半,所以三角形CDO的边长CD是三角形ABO的边长AB的一半,三角形CDO的边CD对应的高是三角形ABO的边AB对应的高的一半,所以三角形CDO的面积是三角形ABO面积的
,所以阴影ACBD的面积是三角形ABO的面积的(1-
)=
,即阴影部分的面积是大六边形的
,由此求出原正六边形面积.
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |

解答:解:因为小正六边形边长均为是大六边形边长的一半,
所以三角形CDO的边长CD是三角形ABO的边长AB的一半,三角形CDO的边CD对应的高是三角形ABO的边AB对应的高的一半,
所以三角形CDO的面积是三角形ABO面积的
,
所以阴影ACBD的面积是三角形ABO的面积的(1-
)=
,
即阴影部分的面积是大六边形的
;
36÷
=48(平方厘米),
答:原正六边形面积为48平方厘米;
故答案为:48.
所以三角形CDO的边长CD是三角形ABO的边长AB的一半,三角形CDO的边CD对应的高是三角形ABO的边AB对应的高的一半,
所以三角形CDO的面积是三角形ABO面积的
| 1 |
| 4 |
所以阴影ACBD的面积是三角形ABO的面积的(1-
| 1 |
| 4 |
| 3 |
| 4 |
即阴影部分的面积是大六边形的
| 3 |
| 4 |
36÷
| 3 |
| 4 |
答:原正六边形面积为48平方厘米;
故答案为:48.
点评:关键是根据题意利用三角形的相似性求出三角形CDO的面积是三角形ABO面积的
,进而求出阴影部分的面积是大六边形的
.
| 1 |
| 4 |
| 3 |
| 4 |

练习册系列答案
相关题目