题目内容
 如图,直角梯形ABCD,四边形AEGF、MBKN都是正方形,且AE=MB,EP=KC=9,DF=PM=4,则三角形DPC的面积为
如图,直角梯形ABCD,四边形AEGF、MBKN都是正方形,且AE=MB,EP=KC=9,DF=PM=4,则三角形DPC的面积为162.5
162.5
.分析:如图所示:连接GN,设正方形边长为x,
(1)通过整个梯形面积-2个三角形面积的办法可以求出S△DPC=x2+13x+
;
(2)又因S△DPC=S△PGN+S四边形DCNG
=(S长方形AFKB-S梯AFGP-S梯BKNP)+(S梯DCKF-S△DFG-S△KCN)=
+
;
通过2个式子联立可以求出x的值,从而问题得解.

(1)通过整个梯形面积-2个三角形面积的办法可以求出S△DPC=x2+13x+
| 97 |
| 2 |
(2)又因S△DPC=S△PGN+S四边形DCNG
=(S长方形AFKB-S梯AFGP-S梯BKNP)+(S梯DCKF-S△DFG-S△KCN)=
| 13x |
| 2 |
| 169 |
| 2 |
通过2个式子联立可以求出x的值,从而问题得解.

解答:解:设正方形边长为x
(1)整个梯形面积-2个三角形面积=S△DPC
=(x+4+x+9)×(x+9+x+4)÷2-(x+4)×(x+9)÷2×2
=(2x+13)×(2x+13)÷2-(x+4)×(x+9)
=2x2+26x+
-x2-13x-36
=x2+13x+
;
(2)连接GN,S△DPC=S△PGN+S四边形DCNG
=(S长方形AFKB-S梯AFGP-S梯BKNP)+(S梯DCKF-S△DFG-S△KCN)
=[x(2x+13)-(x+x+9)×x÷2-(x+x+4)×x÷2]+[(4+9)×(2x+13)÷2-4x÷2-9x÷2]
=13x+
;
通过2个式子联立:x2+13x+
=13x+
;
x2=36,
x=6;
所以S△DPC=13×6+
=78+84.5
=162.5.
答:三角形DPC的面积为 162.5.
故答案为:162.5.
(1)整个梯形面积-2个三角形面积=S△DPC
=(x+4+x+9)×(x+9+x+4)÷2-(x+4)×(x+9)÷2×2
=(2x+13)×(2x+13)÷2-(x+4)×(x+9)
=2x2+26x+
| 169 |
| 2 |
=x2+13x+
| 97 |
| 2 |
(2)连接GN,S△DPC=S△PGN+S四边形DCNG
=(S长方形AFKB-S梯AFGP-S梯BKNP)+(S梯DCKF-S△DFG-S△KCN)
=[x(2x+13)-(x+x+9)×x÷2-(x+x+4)×x÷2]+[(4+9)×(2x+13)÷2-4x÷2-9x÷2]
=13x+
| 169 |
| 2 |
通过2个式子联立:x2+13x+
| 97 |
| 2 |
| 169 |
| 2 |
x2=36,
x=6;
所以S△DPC=13×6+
| 169 |
| 2 |
=78+84.5
=162.5.
答:三角形DPC的面积为 162.5.
故答案为:162.5.
点评:此题属于奥数题,难度较大,依据其他图形的面积和或差表示出所求图形的面积,再联立方程即可求解.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目

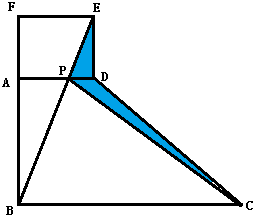 如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是( )平方厘米.
如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是( )平方厘米.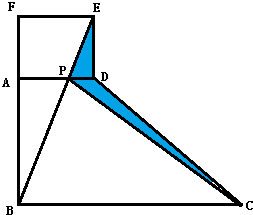 如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是平方厘米.
如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是平方厘米.