Question

如图，正△ABC的面积是1994，P为其中一点，分别连接P与三个顶点，再过P点分别作三条边的垂直线段．在所构成的三角形中，甲的面积为264，求乙丙的面积之和．

Answer 1

考点：三角形的周长和面积

专题：平面图形的认识与计算

分析：过P点分别作三条边的平行线，根据等底等高的三角形面积相等和平行四边形的性质可得甲的面积+乙的面积+丙的面积=正△ABC的面积的一半即可求解．

解答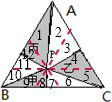： 解：如图所示，过P点分别作三条边的平行线，
由图形可知，1的面积=2的面积，3的面积=4的面积，5的面积=6的面积，7的面积=8的面积，9的面积=10的面积，11的面积=12的面积，
故甲的面积+乙的面积+丙的面积=正△ABC的面积的一半，
1994÷2-264
=997-264
=733．
答：乙丙的面积之和是733．

点评：考查了三角形的面积，本题关键是添加辅助线，以及对等底等高的三角形面积相等的知识点的理解和掌握．