题目内容
某校组织甲、乙两班去距离学校30公里处参观,学校有一辆交通车,只能坐一个班,车速每小时45公里,人行速度每小时5公里,为了使两班同学尽早到达,他们上午8时同时从校出发,那么两班到达参观地点是上午
约9
约9
时33
33
分20
20
秒.分析:要使两班同学尽早到达,应使两班同学始终在行走,且在中途及终点没有等待最省时间.
如图设A是学校,D是目的地.甲班先乘车到C地下车后步行,空车自C返回在途中B处遇到从A步行到B的乙班,乙班同学在B处乘车与步行的甲班同时到达D.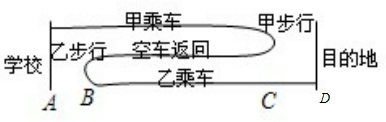
因车速与人速之比为45:5=9:1,故AC+CB(车行路程)与AB之比为9:1.故AC=5AB.又显然有CD=AB(否则两班不能同时到达).故有AB=CD=30÷(5+1)=5(公里),AC=5AB=25(公里).车行总路程为AC+CB+BD=25+20+25=70(公里)总时间为70÷45=1
(小时),即大约在上午9时33分20秒到达.
如图设A是学校,D是目的地.甲班先乘车到C地下车后步行,空车自C返回在途中B处遇到从A步行到B的乙班,乙班同学在B处乘车与步行的甲班同时到达D.

因车速与人速之比为45:5=9:1,故AC+CB(车行路程)与AB之比为9:1.故AC=5AB.又显然有CD=AB(否则两班不能同时到达).故有AB=CD=30÷(5+1)=5(公里),AC=5AB=25(公里).车行总路程为AC+CB+BD=25+20+25=70(公里)总时间为70÷45=1
| 5 |
| 9 |
解答:解:如图,设A是学校,D是目的地.甲班先乘车到C地下车后步行,空车自C返回在途中B处遇到从A步行到B的乙班,乙班同学在B处乘车与步行的甲班同时到达D.;9
则AC+CB:AB=45:9=9:1.
AB+BC=AC,
AB+BC+BC+AB=1+9=10,
2(AB+BC)=10,
AB+BC=5,
故AC=5AB.又显然有CD=AB,
所以,AB=CD=30÷(5+1)=5(公里),
AC=5AB=25(公里).
BC=4AB=4×5=20(公里),
车行总路程为25+CB+BD=25+20+25=70(公里),
总时间为70÷45=1
(小时),
即约1小时33分20秒.故大约在上午9时33分20秒到达.
故答案为:9时33分20秒.

则AC+CB:AB=45:9=9:1.
AB+BC=AC,
AB+BC+BC+AB=1+9=10,
2(AB+BC)=10,
AB+BC=5,
故AC=5AB.又显然有CD=AB,
所以,AB=CD=30÷(5+1)=5(公里),
AC=5AB=25(公里).
BC=4AB=4×5=20(公里),
车行总路程为25+CB+BD=25+20+25=70(公里),
总时间为70÷45=1
| 5 |
| 9 |
即约1小时33分20秒.故大约在上午9时33分20秒到达.
故答案为:9时33分20秒.
点评:本题通过画图解答能比较直观的体现出车行路程与步行路程之间的数量关系.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目