题目内容
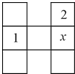 将数码1~7逐一填入图的方格内,使得水平方向的3个方格内的数码和与每个竖直方向的3个方格内的数码和都相等.数码1与2已被填入图示的格子内,那么x可以有
将数码1~7逐一填入图的方格内,使得水平方向的3个方格内的数码和与每个竖直方向的3个方格内的数码和都相等.数码1与2已被填入图示的格子内,那么x可以有2
2
个不同的值.分析:因为横竖共有3个和,而1和x被计算了两次,所以(1+2+…+7+1+x)应是3的倍数,由此进行推算x的值.
解答:解:1+2+3+4+5+6+7+1+x,
=29+x,
29+x的值是3的倍数;
那么:x可以是1,4,7;
当x=1时,与已知的数有1相矛盾,舍去.
当x=4时,幻和就是(29+4)÷3=11;
这个幻方就是:
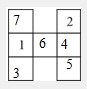
当x=7时,幻和就是(29+7)÷3=12;
这个幻方就是:
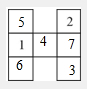
x一共有2种取值.
故答案为:2.
=29+x,
29+x的值是3的倍数;
那么:x可以是1,4,7;
当x=1时,与已知的数有1相矛盾,舍去.
当x=4时,幻和就是(29+4)÷3=11;
这个幻方就是:

当x=7时,幻和就是(29+7)÷3=12;
这个幻方就是:

x一共有2种取值.
故答案为:2.
点评:本题关键是得出所有数的和再加上1和x是3的倍数,由此找出x可能的取值.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目